The One About Trigonometry | MCAT Tips and Tricks

Last Updated on June 23, 2022 by Laura Turner

I’m guessing that by this point in your MCAT preparation you feel like you’ve parked a dump truck full of information next to your desk and shoveled facts into your brain until its about ready to burst. And then you hit that physics problem. The one that requires you to know the sine – or is that cosine? – of 60 degrees.

You search through your mental hard drive for references to trigonometry.  There’s something about SOH CAH TOA… and a² and b².  Oh dear.  Something else to add to the “to memorize” list that’s growing to the thickness of your organic chemistry textbook.

There are lots of videos and articles about tricks for memorizing sine and cosine values, and they are a good starting point, but they aren’t actually that helpful for the MCAT. (We’ll see why later).  All you really need to memorize to do any trigonometry calculation on test day is “syne – point 5, point 7, point 9”. That’s it! Let’s see how this works…

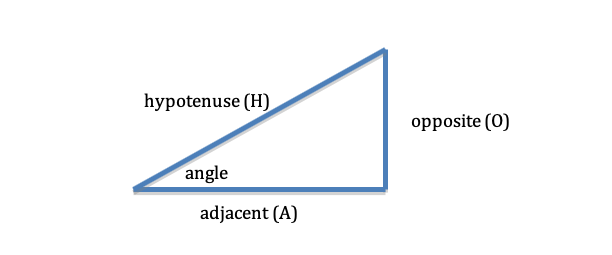
In the physics section of the MCAT, you will need to be able to do calculations with the sine, cosine, and tangent of five degree measures – 0°, 30°, 45°, 60° and 90°. If students remember anything about trigonometry, it’s probably SOH CAH TOA (see below), which reminds us that the sine (S) of an angle is equal to the length of the opposite side of the triangle (O) divided by the hypotenuse (H), the cosine (C) of an angle is equal to the adjacent side (A) divided by the hypotenuse (H) and the tangent (T) equals the opposite side (O) divided by the adjacent side (A).

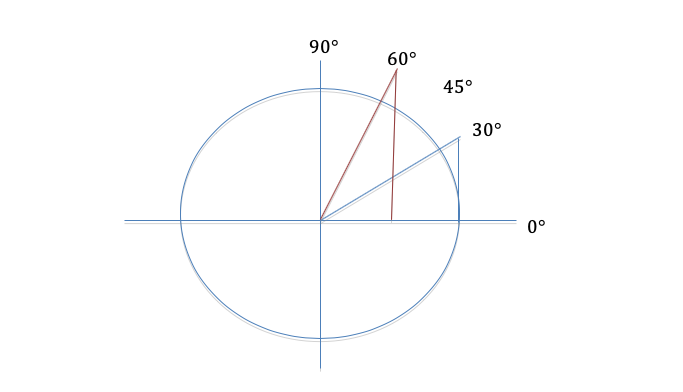
In the picture below, we see two right triangles inscribed over a unit circle: one with its hypotenuse at an angle of 30° with the x-axis and one with its hypotenuse at an angle of 60° with the x-axis. Because sine = opposite/hypotenuse (SOH), the sine of an angle relates the length of the side of the triangle in the y-direction with the hypotenuse. To remember this, it can be helpful to think of “sine” and “y” having similar sounds. That’s why we write “sine” as “syne” in the rhyme.

As you increase the degree of the angle, the length of the triangle in the y-direction increases, as does the sine of the angle. Sin(0°) = 0 because the “triangle” would have no length in the y-direction, and sin(90°) = 1 because the “triangle” would have all of its length in the y-direction.

Cosine describes the ratio of the length of the triangle in the x-direction and follows a similar patter except backward.  As the angle increases, the length of the triangle in the x-direction decreases, as does the cosine of the angle. The cosine of 0° = 1 and the cosine of 90° = 0.

What about the values for sine and cosine for the rest of the angles? Here’s where the point 5, point 7, point 9 part of the rhyme come in.

Let’s begin with sine or “syne” from the rhyme.  The trick that people often teach to memorize the sine of common angles is to begin by writing an empty square root sign divided by 2.

Now, under the square root sign, write the numbers 0, 1, 2, 3 and 4 in order.

Some of these fractions simplify nicely to decimals, but the sine of 45° and 60° won’t.  

Most videos and articles teaching this topic leave you here, but because you don’t have the luxury of working with a calculator, memorizing quantities like 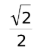doesn’t really help very much. It is better instead to memorize decimal approximations of 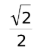and 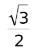, which is where the rhyme comes in. 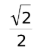≈ 0.7 and 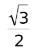≈ 0.9.  

If you have to do a trig calculation with a sine, you can quickly jot down sin(0°) = 0, sin(90°) = 1 and remember the rhyme, “syne – point 5, point 7, point 9” (again “syne” because sine is telling us about the y-direction of the triangle).

If you look back at the unit circle, you see that the cosine values for each of these angles are just the reverse of the sine values. So the cosine of 0° = 1, cosine of 30° = 0.9, etc. If you need the cosine, you can just jot down the values of sine and then put them in the reverse order, no memorization necessary.

Finally, if you need the tangent, divide sine by cosine. If you have any trouble remembering what to divide by what, sine is already above cosine in the table, so you can think of the dividing line between the two as the fraction bar.  

The tangent of 0°, 45° and 90° are easy to calculate. For the tangent of 30° and 60°, you can get a “close enough” answer by approximating 0.9 with 1.

The actual value of tangent(30°) ≈ 0.57 and tangent(60°) ≈ 1.7.

Whew.  With all of that fresh in our minds, let’s do a sample problem:  

A child begins to pull a toy behind her with a force of 8 N at an angle of 45° with the ground. The initial acceleration of the toy is 2 m/s².  What is the mass of the toy?

a) 1.63kg
b) 2.84kg
c) 4.00kg
d) 6.21kg

The formula relating force, mass and acceleration is F = Ma. Because we want to use force and acceleration to find the mass, we divide both sides by the acceleration to arrive at the formula M = F/a.

As with many physics problems, it’s helpful to draw a sketch of what is going on. Here’s a kid pulling a toy… um… something or other.

Both force and acceleration are given in the problem; however, the 8 N of force being applied to the toy is at a 45° angle. Some of that force is pulling the toy in the y-direction, and some of the force is pulling it in the x-direction. Because the problem is asking about the toy being pulled along the ground and not up into the air, we’re interested in the x-component of the force.

We first remember our rhyme, “syne – point 5, point 7, point 9” and know that we are going to be using cosine in this problem, not sine. Therefore, to calculate the x-component of the force, we have F_x = F * cosine(45°). A quick look at our table of sine and cosine values shows that cos(45°) = 0.7 so F_x = F * cosine(45°) = 8 * 0.7 = 5.6. (Know your multiplication tables!)

Filling in the formula M = F/a with our newly calculated F_x from the problem, we get M = 5.6/2 ≈ 6/2 = 3kg, which is closest to answer b) 2.84kg.

Another example:

A tow truck is pulling 25,000 kg car with a tow hook that meets the car at an angle of 30° with the ground. How much force must the tow truck use to pull the car with an initial acceleration of 3 m/s²?

a) 33,612N
b) 50,319N
c) 75,000N
d) 86,206N

Here’s a quick picture of our scenario.

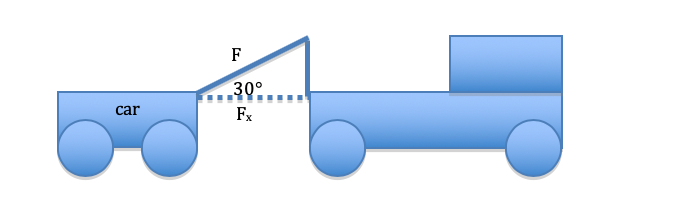
Here, the force needed to pull the car in the x-direction can be calculated using the formula F_x = Ma.  

In this scenario, we’re given the mass of the car and the acceleration in the problem. The required force in the x-direction is F_x = 25,000kg * 3 m/s² = 75,000N. Expressed in scientific notation, this is 7.5 x 10⁴ N.  

However, because the truck is towing the car at an angle of 30°, the truck is going to need more force than that, because it is acting on the car in both the x- and y-directions.

In the previous problem, we saw that F_x = F * cos(Θ) where Θ is the degree of the angle, which in this case is 30°. Reviewing our table of sine and cosine values, we see that cos(30°) ≈ 0.9.  Expressed in scientific notation, this is 9 x 10^-1.

To solve for F, divide each side of the equation by cos(Θ), which gives the formula  .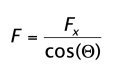

We re-express F_x as 75 x 10³ N rather than 7.5 x 10⁴ N to make the division problem a little easier.

The result is 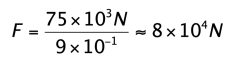which is closest to answer d). Note that this has to be the correct answer because it’s the only answer choice that was greater than 75,000N.

Make sure to check out the rest of the MCAT Tips and Tricks Series:

• Part I – Converting between units in the metric system
• Part II – Calculating logarithms without a calculator
• Part III – Using approximations to tackle complex calculations
• Part IV – Unit conversions in eight easy steps