Last Updated on June 23, 2022 by Laura Turner
Unit conversion questions are so common on the MCAT that they deserve their own post. Test authors love having you calculate how many moles of this are in a kilogram of that. Bonus points (for them!) if the process takes at least four steps.
In a previous post, we’ve shown an easy method for doing metric conversions. We’re going to make use of that information now, so I’d recommend reading it again if you need a refresher. In this article we will turn our attention to conversions between other units such as converting miles per hour to meters per second or milligrams per cubic centimeter to kilograms per cubic meter.
Unit conversions are deceptively difficult because they don’t require any specialized math knowledge like logarithms or trigonometry. However, without a plan, it’s easy to get tangled up wondering what step to take next. Fortunately, if you follow these easy steps, unit conversions become a breeze.
And, yes, there are a lot of steps. However, in my experience as a math teacher, it is better to break things down as simply as possible in the beginning. With a little practice, the process will speed up.
We’ll begin by illustrating the steps for doing unit conversions with a simple example and then work through some more complex problems, showing how the same rules apply.
Example 1: A car is driving 45 miles per hour. What is the car’s speed in kilometers per hour? Hint: There are about 0.62 miles in a kilometer.
a) 0.63 km/hr
b) 7.38 km/hr
c) 27.9 km/hr
d) 72.6 km/hr
Step 1: Write the information given in the problem fraction on the left hand side of your note board and the desired units on the right side.
Step 2: Look at the units in the numerator and determine if they match. They don’t, which means we will have to convert between miles and kilometers. Don’t worry about the denominator at first. We’ll get to that later.
Step 3: Begin to set up a multiplication problem between the original quantity and a conversion factor that relates miles and kilograms. You want the conversion factor to have kilometers as the units of the numerator because those are the desired units for the answer and miles as the denominator because you want to be able to cancel out that unit in the final answer. Always—this is key—always write the units at every step.
Step 4: Now fill in amounts for the numerator and denominator of the conversion factor so the quantities are equal. Remember that unit conversion works based on the principle that any number multiplied by 1 is still equal to itself. The hint in the problem tells us that 1 kilometer is equal to 0.62 miles (thus 1km/0.62mi = 1), so you can substitute these quantities in for the question marks in the previous step.
Now cross-multiply and cancel out “miles”, leaving kilometers in the numerator and hour in the denominator.
Step 5: Look at the units in the denominator and determine if they match. They do! You don’t have to do any more unit conversion. At this step, the answer is
Step 6 and 7: Would be to convert the units of denominator the same way you converted the units of the numerator in steps 2 and 3. You don’t have to do that, though, so you can skip to–
Step 8: Complete any arithmetic so you can select the correct answer. Remember to approximate rather than getting stuck on finding the exact solution.
Which is closest to the correct answer d) 72.6 km/hr.
Now let’s look at another example where both the numerator and denominator must be converted.
Example 2: What is 3.2 g/mL expressed in kg/m3?
a) 3.2 x 10-6 kg/m3
b) 3.2 x 10-3 kg/m3
c) 3.2 x 103 kg/m3
d) 3.2 x 106 kg/m3
Step 1: Set up the beginning and end of the problem.
Step 2: Note that the numerator units don’t match.
Step 3: Begin to convert the numerator. Note that kg is in the numerator and g is in the denominator so the final units will be expressed in kg and the g will be cancelled when you cross-multiply.
Step 3: From our previous work with metric conversions, we know that 1 kg is equal to 1000g. It is nearly always true that it is easier to multiply and divide numbers written in scientific notation so it makes sense to express 3.2 and 1000 as 3.2 x 100 and 1 x 103, respectively, to make the arithmetic easier.
Step 4: Cancel “grams” in the numerator and denominator and simplify the fraction using the rules of exponents (recall that, to divide two numbers written in scientific notation, divide the significands and subtract the exponent in the denominator from the exponent in the numerator).
Step 5: Look at the units in the denominator and determine if they match. They do not. We will need to convert mL to m3.
Step 6: Set up the conversion factor for mL to m3. This conversion is a little trickier than the last two because most students have memorized the relation of L to m3 rather than mL to m3. However, this just means you will need two conversion fractions rather than one. First you’ll convert from mL to L and then from L to m3.
Step 7: Fill in the correct amounts that relate mL to L and L to m3.
It’s helpful to walk through the step of cancelling out the intermediate units to make sure you’ve done the problem correctly. Remember, always write out all the units.
Step 8: Expressing 1000 in the second two fractions in scientific notation as 1 x 103 will help you complete the problem. Remember that to multiply numbers expressed in scientific notation, multiply the significands and add the exponents.
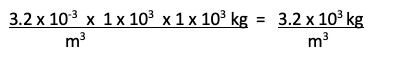
Which is answer c).
Let’s finish with one more problem similar to what you might see on the MCAT.
Example 3: A scientist takes a water sample from an underground lake and distills it, resulting in the separation of distinct compounds. He finds 3.4 x 1023 molecules of Compound 1, which has a mass of 0.3 kg. What is the molar mass of the compound?
a) 5.3 x 10-2 g/mol
b) 1.9 x 10-2 g/mol
c) 1.9 x 102 g/mol
d) 5.3 x 102 g/mol
Step 1: This question is more difficult because the units aren’t given to us explicitly in the problem. We can infer from the question that the mass of the compound is 3.4 x 1023 molecules per 0.3 kg and that the desired units are g/mol because all the answers are expressed in those units.
Step 2: The units in the numerator don’t match. In fact, the measurement in the numerator (mass) and the measurement in the denominator “flip” between what is given in the problem and the answer. Let’s start by making the problem simpler and converting from molecules/kg to mol/g and then converting back to g/mol in step 8.
Step 3: The conversion factor will have mol in the numerator and molecules in the denominator.
Step 4: Use Avogadro’s number, which defines the quantity of a mole of a substance.
Luckily, both the 1023 and the “molecules” units cancel out when you cross-multiply.
You can also do some simple arithmetic to clean things up, recognizing that .3 x 6 is ≈ 2.
Steps 5 – 7: The quantities in the denominator don’t match so you need to convert from kg to g using the metric conversion mnemonic. Represent 1000g in scientific notation as 1 x 103 to make the arithmetic easier later.
Step 8: Instead of mol/g, the correct answer is in g/mol so all that is left to be done is to flip the fraction and do the final bit of arithmetic and approximation.
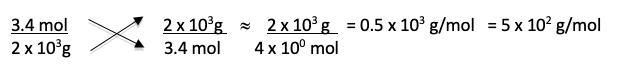
Which is closest to answer d) 5 x 102 g/mol.
Make sure to check out the rest of the MCAT Tips and Tricks Series:
- Part I – Converting between units in the metric system
- Part II – Calculating logarithms without a calculator
- Part III – Using approximations to tackle complex calculations
- Part V – The one about trigonometry
Chelsea Myers, M.Stat, is the author of the MCAT Math eBook series available at www.mcatmath.com. After a decade-long career as a research biostatistician in the Department of Ophthalmology and Visual Sciences at the University of Wisconsin – Madison, she is currently a professor of mathematics, statistics and biostatistics at Rollins College and Valencia College in Florida. She lives with her husband and three sons in the Orlando area.