Using Approximation To Tackle Complex Calculations | MCAT Tips & Tricks

Last Updated on June 24, 2022 by Laura Turner

One of the most difficult things about taking the MCAT is that it is both a marathon and a sprint. The test itself is more than 6 hours long, yet students have to work through each section at a brisk pace in order to answer every question. There are many strategies for managing time on different types of MCAT questions, and math is no exception.

Perhaps the most important thing to keep in mind when solving math problems on the MCAT is that students are not expected to calculate the correct answer to a question but rather to identify the correct answer from a list of choices.

The authors of the test know that some of the answers are actually impossible to calculate without technology, and the answer choices will reflect that. Most potential answers will be so far apart that, if you understand the scientific principles being tested, you will be able use smart approximation to arrive at an answer that is “close enough” to select the correct one.

One thing that can slow students down is trying to multiply or divide two numbers with long trailing decimals. This is almost never necessary. There are two strategies that will allow you to avoid long, tedious calculations by hand and find a solution quickly and efficiently.

The first is rounding to the nearest whole number. This works best for calculations with small numbers because students are expected to be able to multiply and divide integers between 1 and 10. That means feeling just as comfortable recalling 7 x 8 now as you did when you learned the multiplication tables in elementary school.

Some examples:

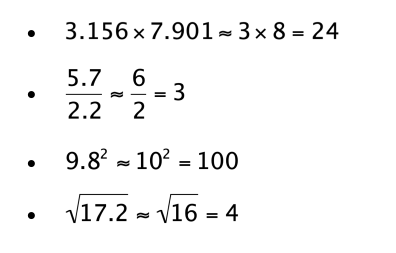
The second strategy is to recognize the numbers you use in daily life that can act as “anchors” for approximation when a problem requires arithmetic with larger numbers.

For example, many students would struggle to solve 500/23 without a calculator. However, if you are accustomed to using a currency with quarters and dollars, doing mental math with the number 25 might not be that difficult.

Rather than trying to answer 500/23, the question becomes “How many quarters are there in $5?” Four quarters in a dollar yields 20 quarters in 5 dollars, and therefore 500/23 ≈ 20.

If, instead, multiples of 20 are more natural to work with, the previous problem could have been approximated using 20 rather than 25. Other potential anchors are 12 (a dozen, 12 hours in a day) and 15 (four 15-minute periods in an hour).

Some examples:

Let’s use these two techniques to solve a difficult-looking exponential decay problem using smart approximation.

At time t = 0 there is a 6 mole sample of a radioactive isotope that is decaying at a rate of 3.9 hr^-1. How many mol of the sample remain after half an hour? (Hint: e^-1.95 ≈ 0.14)

a) 0.02 mol
b) 0.85 mol
c) 2.23 mol
d) 3.65 mol

The equation for exponential decay—which should be memorized—is n = n₀e^-λt, where n is the amount remaining at time t, n₀ is the initial quantity, λis the decay rate and t is the time elapsed.

Substituting in quantities from the problem yields

n = 6e^-3.9(.5)

We can use our first strategy of rounding to a whole number to approximate -3.9 x ½ as -4 x ½ = 2. 

n = 6e^-3.9(.5) ≈ 6e^-2

This equation might seem intimidating to solve without a calculator because of the e^-2 term, but calculations with base e are beyond the scope of the MCAT, which is where the hint comes in. We see that e^-2 ≈  e^-1.95 ≈ 0.14, which will be close enough for us to solve for the correct answer.  Substituting in 0.14 for e^-2 yields

n = 6e^-3.9(.5) ≈ 6 x 0.14

It would be possible, though time consuming, to find an exact answer to this multiplication problem. However, we know it’s not necessary. By using the anchors of minutes and hours, we know that there are four 15-minute quarter-hours in 60 minutes plus two more 15-minute quarter-hours gives us 90 minutes. Therefore,  

n ≈ 6 x 0.14 ≈ 0.90 mol

Glancing at the answer choices, we see that our approximation is actually very close to answer b), which is indeed the correct answer.

Using the two strategies of rounding to the nearest whole number and using everyday anchors for approximation will help you sprint through complex calculations, leaving you with more metal energy so you can power through the marathon that is MCAT test day.

• Part I – Converting between units in the metric system
• Part II – Calculating logarithms without a calculator
• Part IV – Unit conversions in eight easy steps
• Part V – The one about trigonometry